Pythagoras-Calculator
a² + b² = c²
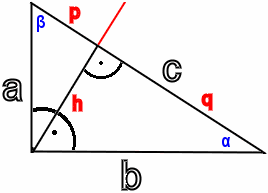
Right Triangle:
Please enter for a, b and c two length values altogether, the third value has to stay empty.
Then click on Calculate, to compute the other values.
The Pythagorean theorem or hypotenuse theorem states that the sum of the squares of the lengths of the two legs a and b is equal to the square of the length of the hypotenuse c. In the language of mathematics: a² + b² = c²
This relationship was known long before Pythagoras, the ancient Babylonians and Indians used it in practice. There is a Babylonian cuneiform script three and a half to four thousand years old that describes the calculation with example values. However, no proof is attempted there. Pythagoras of Samos, who lived in the sixth century BC, is said to have proved the theorem, but this is disputed. Nonetheless, it is named after him. The Pythagorean theorem is a fundamental theorem of Euclidean geometry and one of the most famous mathematical statements of all.
The catheti are the two short sides in a right triangle, which are at the right angle. The hypotenuse is the longest of the three sides, it is opposite the right angle. For example, a right triangle is formed by dividing a rectangle into two opposite corners. The hypotenuse then corresponds to one of the two diagonals in the rectangle. The right angle is a 90 degree angle, which corresponds to a quarter of a circular path. The two catheti are perpendicular to each other. The two angles of the respective cathetus with the hypotenuse are each less than 90 degrees. As in any Euclidean triangle, the sum of all three angles is 180 degrees.
There are hundreds of proofs for the Pythagorean Theorem. Many of these are geometric, they break down the shapes into congruent triangles and then show that the corresponding sizes match.
© Jumk.de Webprojects | Imprint & Privacy
|
