Der Pythagoras-Rechner
a² + b² = c²
Rechtwinkliges Dreieck:
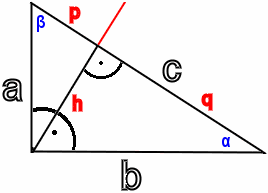
Bitte für a, b und c insgesamt zwei Längenangaben eingeben, der dritte Wert bleibt frei.
Klicken Sie dann auf Berechnen, um die anderen Längen auszurechnen.
Der Satz des Pythagoras oder Hypotenusensatz besagt, dass die Summe der Quadrate der Längen der beiden Katheten a und b gleich des Quadrates der Länge der Hypotenuse c ist. In der Sprache der Mathematik: a² + b² = c²
Diese Beziehung war schon lange vor Pythagoras bekannt, die alten Babylonier und Inder wendeten ihn in der Praxis an. Es gibt eine dreieinhalbtausend bis viertausend Jahre alte babylonische Keilschrift, auf der die Rechnung mit Beispielwerten beschrieben wird. Ein Beweis wird dort allerdings nicht versucht. Pythagoras von Samos, der im sechsten Jahrhundert vor unserer Zeitrechnung lebte, soll den Satz bewiesen haben, dies ist aber umstritten. Dennoch ist er nach ihm benannt. Der Satz des Pythagoras ist ein fundamentaler Satz der euklidischen Geometrie und eine der berühmtesten mathematischen Aussagen überhaupt.
Die Katheten sind die beiden kurzen Seiten in einem rechtwinkligen Dreieck, welche am rechten Winkel anliegen. Die Hypotenuse ist die längste der drei Seiten, sie liegt dem rechten Winkel gegenüber. Ein rechtwinkliges Dreieck entsteht zum Beispiel, wenn man ein Rechteck durch zwei gegenüberliegende Ecken teilt. Die Hypotenuse entspricht dann einer der beiden Diagonalen in dem Rechteck. Der rechte Winkel ist ein Winkel mit 90 Grad, dies entspricht dem Viertel einer Kreisbahn. Die beiden Katheten stehen senkrecht aufeinander. Die beiden Winkel der jeweiligen Kathete mit der Hypotenuse sind jeweils kleiner als 90 Grad. Die Summe aller drei Winkel ist - wie in jedem euklidischen Dreieck - 180 Grad.
Es gibt hunderte von Beweisen für den Satz des Pythagoras. Viele davon sind geometrisch, sie zerlegen die Formen in kongruente Dreiecke und zeigen dann, dass die entsprechenden Größen übereinstimmen.

© Jumk.de Webprojekte | Rechneronline | Impressum & Datenschutz
|
